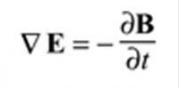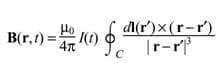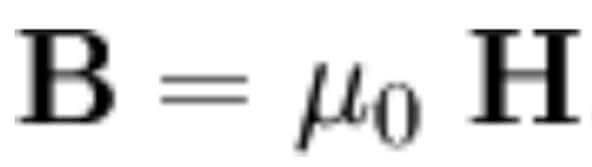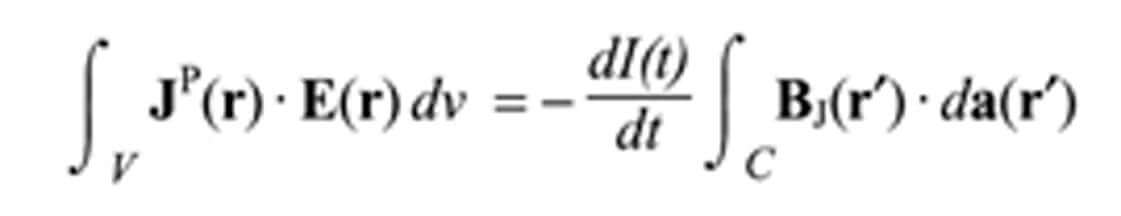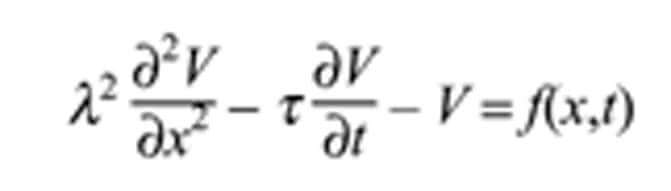Физические основы ТМС

С помощью изменяющегося магнитного поля можно возбуждать нейроны головного мозга. При ТМС для этого используется катушка, которая располагается над головой пациента. В катушке изменяется интенсивность импульсов тока (показатель I(t)). Источник активации – электрическое поле Е, индуцируемое в ткани, согласно закону Фарадея:

Здесь μо – магнитная проницаемость в вакууме (Гн/м). Через магнитную проницаемость связаны вектор магнитной индукции В и вектор магнитного поля Н:

Схема образования импульса ТМС

Импульс тока образуется в цепи содержащей конденсатор, соединённый последовательно с катушкой и тиристором. Конденсатор заряжается до 2-3 кВ, после чего тиристор открывается, и конденсатор разряжается через катушку. Длительность полученного импульса д.б. около 300 мс и амплитуду около 5-10 кА.

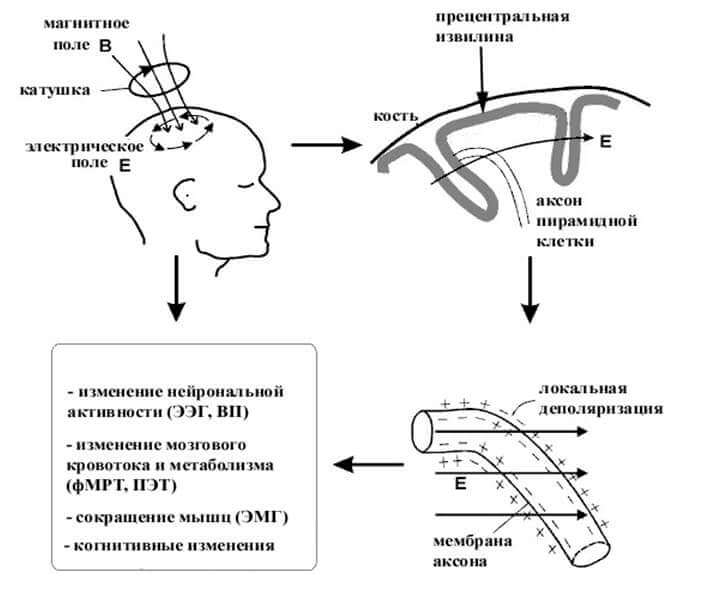
На рис.1 показана цепь событий, происходящих при ТМС. Электрическое поле Е сильнее около катушки и стимулирует кортикальную область диаметром в несколько сантиметров. Импульс при ТМС обеспечивает когерентный разряд нейронов в стимулируемой области так же, как разряды нейронов воздействуют на синаптический вход. На микроскопическом уровне поле Е влияет на трансмембранное напряжение нейронов и, таким образом, на чувствительные к напряжению ионные каналы.

При стимуляции моторной коры периферические эффекты могут наблюдаться при помощи регистрации ЭМГ. Кроме того, при ТМС могут быть и когнитивные изменения (эмоции, память, мотивация).

Моделирование магнитной стимуляции

Математические модели магнитной стимуляции наиболее важны для исследования механизмов стимуляции при подготовке экспериментов и разработке эффективных инструментов. Но проблема в том, что корректное решение этой задачи связано с решением системы уравнений Максвелла, и в общем виде решить эту систему пока не удалось. Некоторые частные решения могут быть такими.

Сферическая модель головы

В МЭГ широко используется сферическая модель для моделирования проводниковой геометрии головы. Было показано, что сферическая модель подходит для внешних частей головы.  Сферическая модель при ТМС должна использоваться так, чтобы сфера подходила по локальному радиусу кривизны внутренней поверхности черепа возле области интереса.

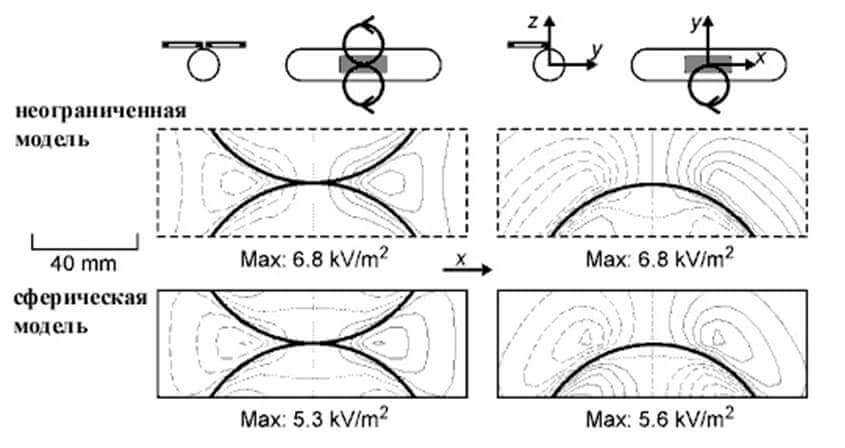
На рис.2 показаны величины индуцированного Е в неограниченных и сферических моделях для круглых и 8-образных катушек.

Когда круглая катушка расположена над головой без наклона (рис.2в, ось катушки тангенциальна к сферической поверхности), электрическое поле, индуцируемое в сфере, меньшее, чем в неограниченной модели. В отсутствие границ максимальное значение поля одинаково для тангенциальной и прямой катушки (рис.2а и 2в, вверху).

Эффекты границ исчезают для любой катушки, если её ось прошла через центр сферы. Это является одной из важных причин того, почему моторные ответы при ТМС с круглой катушкой более легко выявить при её расположении на вертексе, чем при других локализациях.

Закон Ампера-Лапласа, который является непрерывной копией Био-Савара в уравнении 2, указывает на то, что во всех аксиально симметричных проводниковых формах индуцируемая напряжённость Е вдоль любой оси вращения на этой оси равна нулю. Это означает, что Е никогда не ориентируется по отношению к центру сферы.

Моделирование конечностей и спинного мозга

Объёмные проводники цилиндрической формы могут быть использованы, как  модели конечностей. Показаны решения для Е и его градиента ∂Εx/∂x в вытянутом сфероиде, как для неограниченных, так и полуограниченных проводниках. Аналитическое решение также пригодно и к бесконечно-вытянутым круговым цилиндрам. Ограниченно вытянутые цилиндры так же были проанализированы численно.

При периферической магнитной стимуляции  активирующая способность Е измеряется её градиентом вдоль аксона, ∂Εx/∂x. Рис.3 показывает ∂Εx/∂x, индуцируемое в сфероиде и неограниченной среде для круглой и 8-ми образной катушки.

∂Εx/∂x – схож в различных моделях, но его величина меньше в сфероиде. Показано, что при обычно используемой ориентации катушки поле в проводнике цилиндрической формы составляет 70-80 % от поля в неограниченном объёме. Полезность упрощённых моделей цилиндрической формы невелика, так как их вычисление требует затрат времени, а неточность неограниченной модели для оценки формы Е мала.

Кости и негомогенность в спинальной нейрогеометрии сильно влияют на индуцируемый Е. Хорошо проводящая цереброспинальная жидкость весьма ослабляет поле в менее проводящем спинном мозге. Это объясняет, почему современные магнитные стимуляторы не могут возбуждать нейрональные и проводящие элементы спинного мозга.

Связь между ТМС и МЭГ

ТМС – по существу, магнитоэнцефалография (МЭГ) наоборот, в которой используется ряд высокочувствительных катушек для измерения магнитного поля, генерированного электрическими токами, связанного с активацией нейронов.

Вследствие принципа взаимности некоторые результаты, полученные для МЭГ, будут приемлемы для ТМС, и наоборот. Е, индуцируемое в мозге с помощью ТМС, может быть получено с помощью тех же формул, которые в МЭГ дают чувствительный сигнал катушки благодаря интракраниальным токам. Теоретическая взаимосвязь образована теоремой взаимности:

Оба вычисления подчиняются одной геометрии. Взаимность имеет место как для линейного и неоднородного пространства, так и для анизотропного пространства с симметричными тензорами проводимости и магнитной проницаемости.  Более того, необходимо, чтобы ток I(t) был низкой частоты.

Форма проводящих границ головы, спинного мозга и конечностей может быть получена с помощью МРТ. Эта информация может быть использована для реконструкции реалистичных моделей проводящей геометрии, несмотря на то, что МРТ не даёт оценки проводимости.

При помощи МКЭ-моделирования было изучено влияние анизотропии и негомогенности на ТМС-индуцированное электрическое поле.

Предпочтительное направление Е при анизотропиях было вдоль направления уменьшения проводимости. Пик значения Е в гетерогенной тканевой модели был 50-100% от значения в гомогенной неограниченной модели. Следовательно, области низкой проводимости могут влиять на направление Е в головном и спинном мозге.

Упрощённые модели, такие как сфера, удовлетворительны для объяснения явных характеристик индуцированного электрического поля, особенно, если область интереса поверхностно расположена, а модель геометрии соответствует локальной кривизне тела.

Электрофизиология возбуждения в аксонах

Теоретически электрическое поле Е приводит свободные заряды в движение как в интра-, так и в экстраклеточных пространствах. На практике, однако, основные клеточные механизмы неясны, несмотря на то, что макроскопические электромагнитные поля хорошо изучены. Для моделирования процессов, происходящих при ТМС в аксонах, предложена кабельная модель. Но надо учитывать, что все эффекты, лежащие в основе нейрональной активности пока математически описать нельзя.

Кабельная модель

Поведение трансмембранного потенциала V, измеренное от потенциала покоя, описано с помощью кабельного уравнения:

Уравнение 5 действует при различных формах аксонов, миелинизации и длины. Изменения в аксоне, описанные моделью Hodgkin-Huxley, могут быть описаны кабельным уравнением, но математическая обработка становится нелинейной и усложнённой.

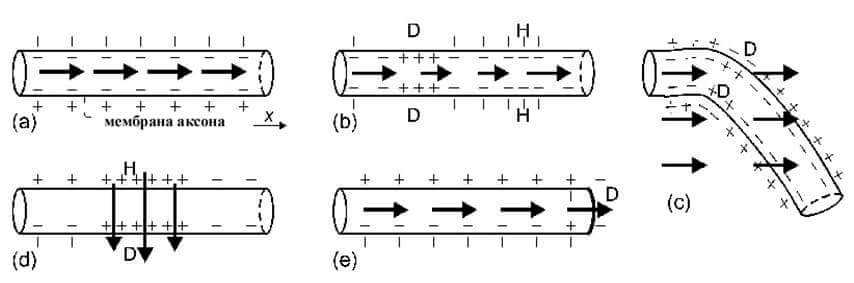
Соотношение механизмов пересечения и градиента поля независимо от размеров аксона. Схематичная иллюстрация поляризации мембраны аксона в пересеченном волокне показана на рис.4.

Геометрические факторы, влияющие на возбудимость

В нервной ткани отмечаются изменения нейрональной возбудимости вследствие различных геометрических факторов, например, наличии окончания аксонов, изгибов, ответвлений, различной толщины и длины. Особенно изгибы и окончания играют ключевую роль при ТМС. Высокоэффективные ∂Εx/∂x значения  достигаются в изгибах даже в гомогенном поле Е. В тонких изогнутых аксонах относительный вклад от пересеченного поля Ет мал при сравнении с ∂Εx/∂x.

Компьютерное моделирование и эксперименты invitro указывают на то, что, если катушку располагать близко к концу аксона, или если аксон короткий (<6-8 см), мембрана аксона наиболее деполяризована в конце волокна параллельного к аксону.